- 星ネズミ
- Mar 11, 2018
いまさらですが逆ポーランド記法への変換
計算機で数式を計算する場合によく取り上げられる逆ポーランド記法への変換方法と逆に中置記法へ変換する方法と注意点についてまとめてみた。

後置記法は逆ポーランド記法とも呼ばれ、数式を計算する場合などによく使われます。この記法が式の計算に都合がよいのは、付属の「逆ポーランド記法での計算図」に示したように、式の順番通りに読めば、計算できるのでプログラムしやすいためです。 逆ポーランド記法は、括弧が必要ないという利点もあります。(1 + 2 )* 3なら1 2 + 3 *という具合です。
一方デメリットとしては、(人間には)わかりにくいという点があります。よく逆ポーランド法は日本語の順と同じ(5 4 + なら5 に 4を加える)なので分りやすいと言われますが、必ずしも一致するわけではないし、1+2*3^4/5-sin(1/2) が1 2 3 4 ^ 5 / * + 1 2 / sin( - になるとかだと、もうお手上げです。
ここでは中置記法を後置記法に変換する手順と、その逆操作と注意点についてまとめてみました。
中置記法を後置記法に変換するアルゴリズムは以下の通りです。
(1)式の要素(数値、演算子など)を最初から順番に取り出す。
(2)数値の場合は、そのまま出力(後ろに空白をつける)
(3)演算子の場合、演算子を保管するスタック(配列やリストなど)に保存するが、すでにスタックに演算子がある場合はそれらと、ここで読んだ演算子の優先度を比較して保存演算子の優先度のほうが高いか同じなら、それらを出力する。
(4)式を最後まで読んだ時、スタック中に残っている演算子を上(後でスタックに保存された方)から順番に出力する。
(5)括弧がある場合は、括弧でくくられた部分を取り出して、その部分にたいして(1)~(4)の操作を実行する。
(6)関数の場合は、引数部分をとりだして上の操作を実行する。最後に関数名(例えばsin( )を出力する。関数名の後に括弧をつけているのは、これが関数だとわかるようにするため。二つの引数を持つ関数の場合なら、例えばfunc(a , b)の場合、a b func( と並べる。
演算子には優先度が、あってこれが大きい方が先に計算されます。優先度は + ,- < * < / < ^ となっています。+と- の優先度は同じですが、/ (除)は、* (乗)より優先度が大きくなっています。^ はべき乗計算です。
このアルゴリズムに従って 1 + 2*3 -4 を実行すると、
(1) 1 を出力 :結果 1
(2) +をスタックに積む
(3)2 を出力する:結果 1 2
(4)* は、+より優先度が高いのでそのままスタックに積む スタック: + *
(5)2 を出力する:結果 1 2 3
(6)- は*より優先度が低いので、スタックの* を出力する。その下の+とは優先度が同じなので+も出力する。出力結果 1 2 3 * +
その後で - をスタックに積む スタック: -
(7) 4を出力、式の最後まで行ったのでスタックに残った - を出力する。最終結果 1 2 3 * + 4 -
以上の結果逆ポーランド記法では、 1 2 3 * + 4 - となります。
なお数値を出力した後、空白を入れているのは、この記法では数値が連続するので、空白(または何らかの文字・印など)で数値間を分けないと、123 が1と2と3なのか1と23なのか、それとも123なのか区別がつかなくなるからです。
このアルゴリズムに基づいた実際のプログラムが付属図にのせたメソッドTransInfixToPostになります。このメソッドの引数にあたえる式は、要素ごと、つまり数値・演算子・括弧や関数、に分解し現れる順番に並べたリストで与えています。この要素は単なる文字列で与えてもいいですが、その場合文字列を読んで、それが数値なのか演算子なのか判断し、演算子の場合、優先度をその都度検索する必要が出てきます。
そこでここでは以下のようなクラスを作って要素の種類や演算子の優先度を、そのフィールドに与えるようにしてあります。
public class FormElement {
public static final int OPETOR_KIND = 0 ;//演算子
public static final int OPERND_KIND = 1;//数値
public static final int FUNC_KIND = 2 ;//関数
public static final int BRACKET_KIND = 3 ;//括弧・閉じ括弧(priorityで区別)
String content;//内容 数値・演算子(+,-,*,/,^)・括弧・関数(sin ,cos,...)
int the_kind ;
int priority;//優先度(演算子)-->関数の場合引数の数を与える
content に演算子なら、+ - * や/、数値なら”1.2”などといた数字(が文字列として)が収められています。メソッドgetContentはcontentをgetThe_kindは the_kindをgetPriorityは priority を返します。次に逆変換つまり逆ポーランド記法から中置記法に変換するアルゴリズムを示します。なおこれは、逆ポーランド記法を使って数式の値を計算する方法とほとんど同じです。
(1)後置記法での式の要素(数値、演算子など)を最初から順番に取り出す。
(2)数値の場合は、用意してあるスタック先頭(一番上)に保存する。
(3)演算子(op)の場合、スタックの上から2番目の内容Aと一番上の内容Bを取り出して、Aとop、Bの順番で文字列を結合する。結果をスタックの上から2番目に保存して一番上は空にする。
関数の場合は、引数が一つなら一番上の内容A、二つなら一番上αと上から二番目までの内容βを取り出して 関数名 + A+ ")"[引数二つの場合は関数名 +β +" ," + α +" ) " ]の順番で文字列を結合する。
(4)以上を読む式要素が無くなるまで続ける。
(5)最後にスタックの内容を取り出すと、それが求める結果
さて、操作(2)のところで文字列を結合するのではなく、演算子によって計算すると、これは数式の値を計算する方法そのものです。ただこのままでは、困る場合があります。
例えば(1 + 2)*3 などの場合、逆ポーランド記法では 1 2 + 3* となりますが、これを上のアルゴリズムで元に戻そうとすると、1+2*3 となります。
従って上のアルゴリズムを括弧が必要な場合に対応出来るようにする必要があります。そのために各要素に優先度を設定します。演算子は既に設定されている値を、数値は演算子より大きな優先度を設定します。そこで(3)に次の操作を追加します。
(3)'取り出した文字列を連結する前に、opとAの優先度を比較する。Aの優先度がopより小さい場合、Aを括弧でくくる。Bについても同じ操作をおこなう。結合して作成したA op Bに優先度を設定するが、これはA、op、Bの中で最小の値に設定する。ただし括弧でくくった要素の優先度は無視(数値とおなじく最大の優先度が設定されているものとする)する。
このアルゴリズムに基づいたプログラムが、メソッドTransPostToInfixです。引数のform_listは逆ポーランド記法での順番に並べられたものです。またcont_save 文字列配列が、上のアルゴリズムで説明したスタックに、あたります。このスタックに収められている各要素の優先度をprio_sav 配列に入れます。
/* 後置表記から中置表記をつくる(文字出力)*/
public static String TransPostToInfix( ArrayList < FormElement > form_list){
int list_size = form_list.size();
int[] prio_sav = new int[list_size];//演算子などの優先度保管(cont_savと対応)
String[] cont_sav = new String[list_size];//文字出力保管場所
int curr_pos = 0;
for(int index = 0 ;index < list_size;index++ ){
FormElement form_elem = form_list.get(index);
int the_type = form_elem.getThe_kind();
switch(the_type){
case FormElement.OPERND_KIND://数値類の場合は単にリストを積む
cont_sav[curr_pos] = form_elem.getContent();
prio_sav[curr_pos] = 10;//優先度の設定はなし(大きな値を設定)
curr_pos++;
break;
case FormElement.OPETOR_KIND://演算子の場合
if(curr_pos >=2){//後置表記が正しければ、いつでも成立のはず
int priority = form_elem.getPriority();
int left_prio = prio_sav[curr_pos-2] ;
int rgt_prio = prio_sav[curr_pos-1];//一番上
String left_term ="" ,right_term ="";
if(left_prio < priority){//括弧をつけて出力
left_term = ( "(" + cont_sav[curr_pos-2 ]+")");
left_prio = 10 ;// ()内を考慮しないようにするため
}else{
left_term = cont_sav[curr_pos-2 ];
}
if(rgt_prio< priority){
right_term = ( "(" + cont_sav[curr_pos-1] +")" );
rgt_prio = 10 ;
}else
right_term =cont_sav[curr_pos-1];
cont_sav[curr_pos-1] ="";//中身なしに
cont_sav[curr_pos-2]=( left_term + form_elem.getContent()+ right_term);
int temp_min = Math.min(left_prio, priority);
prio_sav[curr_pos-2] = Math.min(temp_min, rgt_prio);//最小値
prio_sav[curr_pos-1] = 10;//無効値に
curr_pos--;//スタック位置一つ減らす
}
break;
case FormElement.FUNC_KIND://関数要素出現
if(curr_pos >=1){//後置表記が正しければ、いつでも成立のはず
cont_sav[curr_pos-1] = ( form_elem.getContent() + cont_sav[curr_pos-1] +")" );
prio_sav[curr_pos-1] = 10;//無効値に
//curr_pos 位置に変化なし
}
break;
}
}
System.out.println("curr_pos :" + curr_pos);
if( curr_pos-1 >= 0)
System.out.println("直接変換 "+ cont_sav[curr_pos-1]);
return cont_sav[curr_pos-1];
}
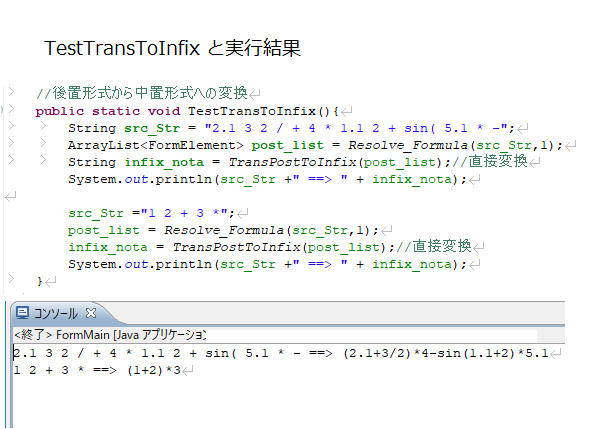
実行結果を、図(メソッドTestTransToInfixと実行結果)に載せてあります。




























Comments
Add your comment